Investors, traders, and market analysts need to understand the relationship between spot prices and futures prices. This relationship is known as spot-futures parity. It plays a vital role in pricing financial instruments and identifying arbitrage opportunities. Let’s explore spot-futures parity implications for market participants.
What is Spot-Future Parity?
Spot-future parity, also known as cost-of-carry, refers to the theoretical equilibrium between the spot and future prices of an asset. This relationship ensures that the futures price reflects the cost of holding the underlying asset until the contract’s expiration date.

In an efficient market, the spot price and futures price should be closely linked, with arbitrageurs quickly eliminating any discrepancies. The parity relationship takes into account various factors such as interest rates, storage costs, and any income generated by the asset (like dividends for stocks or interest for bonds). You can trade on future contracts without risking much.
The Formula for Spot-Futures Parity
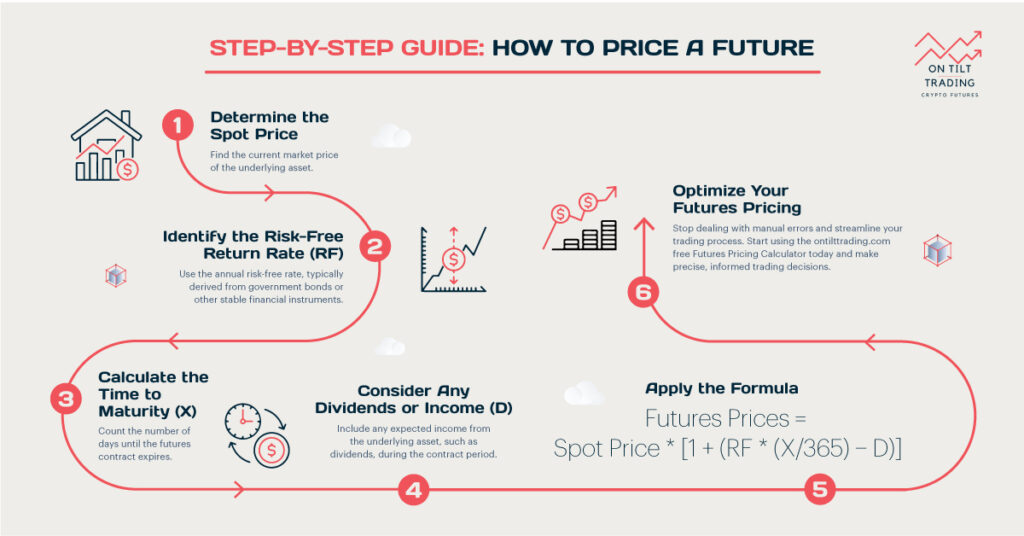
The spot-futures parity formula provides a mathematical representation of the relationship between spot and futures prices. The basic formula is:
F = S * (1 + r)^t
Where: F = Futures price S = Spot price r = Risk-free interest rate (annualized) t = Time to expiration (in years)
This formula assumes that there are no storage costs or income generated by the asset. However, in practice, we often need to account for these factors, especially for commodities or dividend-paying stocks. The expanded formula is:
F = S * (1 + r – y)^t
Where: y = Yield (income) generated by the asset (annualized)
For commodities with storage costs, we can further modify the formula:
F = S * (1 + r + c)^t
Where: c = Storage costs (annualized)
Understanding these formulas is crucial for accurately pricing futures contracts and identifying potential arbitrage opportunities.
Pricing of Existing Futures Contracts
The spot-futures parity formula serves as a theoretical benchmark for pricing futures contracts. In reality, market prices may deviate slightly from this theoretical value due to various factors such as transaction costs, market inefficiencies, and supply and demand dynamics.
When pricing existing futures contracts, market participants consider several factors:
Current spot price
Futures prices are heavily influenced by the current spot price of the underlying asset. This spot price serves as the starting point for futures contracts, reflecting the immediate market value of the asset.
If crude oil is currently trading at $70 per barrel, this sets the baseline for oil futures contracts. It will adjust based on market expectations and other influencing factors.
Interest rates
The prevailing interest rates play a crucial role in futures pricing by affecting the cost of carrying the underlying asset until the contract’s expiration date. Higher interest rates imply greater costs for holding the asset, which can increase futures prices.
For instance, a 3% annual interest rate increases the cost of holding a futures contract for gold over several months. As a result, it influences its price relative to the current spot price.
Time to expiration
Futures prices typically increase with longer contract durations due to the compounding effect of interest rates and other holding costs. Longer periods require more significant financing and storage, leading to higher prices.
For example, a wheat futures contract expiring in six months may trade at a premium compared to one expiring in three months.
Storage costs
In commodities markets, futures prices are impacted by the expenses of storing physical assets until delivery. Storage costs include warehouse fees, maintenance expenses, and insurance, which can significantly influence futures prices. For instance, the price of coffee futures accounts for storage costs related to maintaining coffee beans in warehouses until they are ready for delivery.
Income or yield
Any income generated by the underlying asset, such as dividends for stocks, directly influences futures prices. Expected future cash flows from dividends affect the attractiveness of holding the asset through a futures contract, thus impacting its price.
For example, futures contracts for high-dividend stocks may trade higher to reflect the anticipated income received by holding the stock until contract expiration.
Market expectations
Futures prices are influenced by market expectations regarding future supply and demand dynamics. Anticipated changes in economic conditions, geopolitical events, or weather patterns can impact the perceived future value of the asset, thereby influencing its futures price. For instance, expectations of a poor soybean harvest due to adverse weather conditions may lead to higher futures prices as traders anticipate reduced supply in the future. Need to evaluate trade profitability? Our On Tilt Trading ROI Calculator helps you assess and optimize your portfolio, identifying high-performing investments.
Liquidity and trading volume
The liquidity and trading volume of futures contracts affect their prices. More liquid contracts with higher trading volumes tend to have prices that closely align with their theoretical values, reflecting market sentiment and efficient price discovery. For example, heavily traded futures contracts for major stock indices often trade very close to their theoretical values due to continuous market participation and robust liquidity.
Traders and analysts use the spot-futures parity formula as a reference point to assess whether existing futures contracts are overpriced or underpriced relative to their theoretical values. This analysis can inform trading decisions and help identify potential arbitrage opportunities.
What Is Arbitrage in Futures?
Arbitrage in futures markets refers to the practice of simultaneously buying and selling related financial instruments to profit from price discrepancies. In the context of spot-futures parity, arbitrage opportunities arise when the relationship between spot and futures prices deviates significantly from the theoretical equilibrium.

There are two main types of arbitrage in futures markets:
- Cash-and-carry arbitrage: This occurs when the futures price is higher than the theoretical price derived from the spot-futures parity formula. Arbitrageurs can profit by buying the asset in the spot market, simultaneously selling futures contracts, and holding the asset until the futures contract expires.
- Reverse cash-and-carry arbitrage: This happens when the futures price is lower than the theoretical price. Arbitrageurs can profit by selling the asset short in the spot market, buying futures contracts, and closing both positions at expiration.
Arbitrage plays a crucial role in maintaining market efficiency by quickly eliminating price discrepancies. As arbitrageurs exploit these opportunities, their actions help bring spot and futures prices back into alignment with the theoretical parity relationship.
However, it’s important to note that perfect arbitrage opportunities are rare in practice due to transaction costs, margin requirements, and market frictions. Successful arbitrage often requires significant capital, advanced technology, and quick execution capabilities.
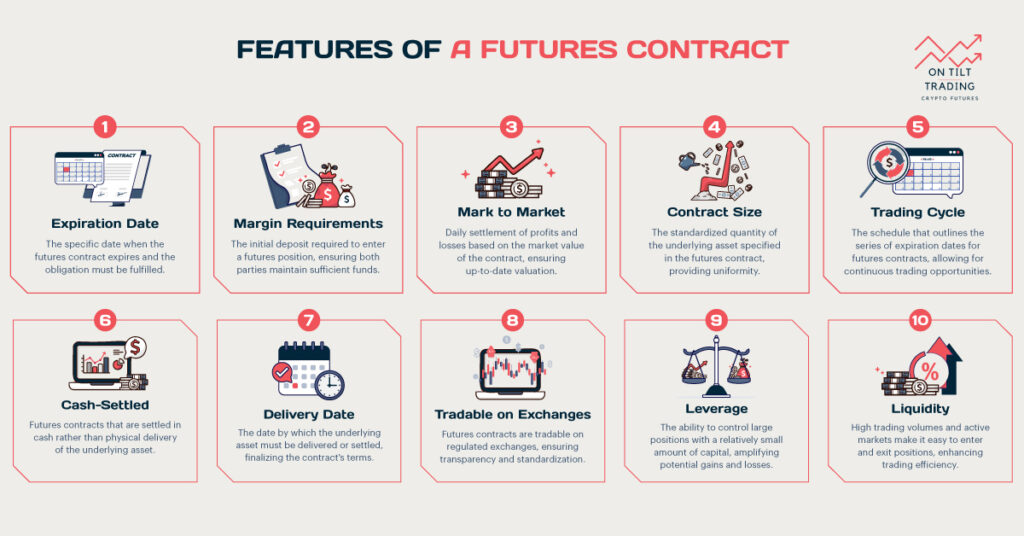
Essentials of Futures Pricing
To fully grasp the concept of spot-futures parity and its implications for futures pricing, it’s essential to understand some key principles:
Fair value
The theoretical futures price derived from the spot-futures parity formula represents the fair value of the contract. Any deviations from this value may present potential trading opportunities.
Convergence
As the futures contract approaches expiration, its price tends to converge with the spot price. This convergence is a fundamental principle of futures markets and helps ensure the effectiveness of hedging strategies.
Contango and backwardation
Contango and backwardation are terms used to describe the relationship between futures prices and the spot price of an underlying asset. Contango occurs when futures prices are higher than the spot price, indicating an upward-sloping futures curve. This situation often reflects higher expected future costs, such as storage and financing, prompting investors to pay more for future delivery.
In contrast, backwardation occurs when futures prices are lower than the spot price, suggesting a downward-sloping futures curve. Backwardation can occur due to immediate demand or supply imbalances, where investors are willing to pay less for future delivery than the current spot price.
Basis
The difference between the spot price and the futures price is called the basis. Understanding basis movements is crucial for hedgers and speculators alike.
Roll yield
When futures contracts are rolled over (i.e., near-term contracts are sold and longer-dated ones are bought), the difference in prices can result in either a positive or negative roll yield.
Leverage
Futures contracts offer significant leverage, as traders only need to put up a fraction of the contract’s value as margin. This leverage amplifies both potential gains and losses.
Mark-to-market
Futures positions are marked to market daily, meaning gains or losses are realized each trading day based on price movements.
Read More: What Is The Formula For Futures Price?
Conclusion
Spot-futures parity is a fundamental concept in financial markets that helps explain the relationship between spot and futures prices. By understanding the formula for spot-futures parity and its implications, market participants can make more informed decisions about pricing, trading, and risk management. You can minimize the risks if you use the right tools.